Problems

1. (8 points) Recall the isPalindromeTR method from the last problem set. Design the boolean isPalindromeLoop(String s) method that solves the problem using a loop. The same restrictions from that problem hold true for this problem.

   Files to Submit: Problem1.java, Problem1Test.java

2. (8 points) Recall the hyperfactorial and hyperfactorialTR problems from the last problem set. (Refer back to that problem set for the hyperfactorial definition.) Design the long hyperfactorialLoop(long n) method that solves the problem using a loop.

   Files to Submit: Problem2.java, Problem2Test.java

3. (8 points) Recall the subfactorial and subfactorialTR problems from the last problem set. (Refer back to that problem set for the subfactorial definition.) Design the long subfactorialLoop(long n) method that solves the problem using a loop.

   Files to Submit: Problem3.java, Problem3Test.java

4. (8 points) Recall the collatz and collatzTR methods from the last problem set. Design the String collatzLoop(int n) method that solves the problem using a loop.

   Files to Submit: Problem4.java, Problem4Test.java

5. (8 points) Recall the collectParenthesizedStrings and collectParenthesizedStringsTR methods from the last problem set. Design the String collectParenthesizedStringsLoop(String s) method, which solves the problem using a loop.

   Like the last problem set, assume there are no nested parentheses, all parentheses are balanced, and each parenthesized string contains at least one character.

   Files to Submit: Problem5.java, Problem5Test.java

6. (20 points) The C programming language contains the atoi "ascii-to-integer" function, which receives a string and, if the string represents some integer, returns the number converted to an integer. Design the int atoi(String s) method that, when given a string \(s\), returns its value as an integer if it can be parsed as an integer, using the following rules:

   • Ignore all leading zeroes and leading non-digits.

   • Upon reading a sign (+ or -), the next character must be a digit.

   • An integer without a sign is assumed to be positive.

   • After reading a digit, if a non-digit is encountered, return the number parsed up to that point.

   • Assume that the bounds of an integer are never exceeded, i.e., all valid integers will be within the bounds of \([-2^{31}, 2^{31}-1]\).

   • If no valid integer is parsed, return 0.

   Writing enough tests is crucial to correctly solving this exercise! We provide some examples below.

   atoi("ABCD")           => 0
   atoi("42")             => 42
   atoi("000042")         => 42
   atoi("004200")         => 4200
   atoi("ABCD42ABCD")     => 42
   atoi("ABCD+42ABCD")    => 42
   atoi("ABCD-42ABCD")    => -42
   atoi("000-42000")      => -42000
   atoi("000-ABCD")       => 0
   atoi("-+-+1234")       => 0
   atoi("-A1234")         => 0
   atoi("000+42ABCD")     => 42
   atoi("8080*8080")      => 8080
   

   Warning 1: you are not allowed to use Integer.parseInt or similar methods that trivialize the problem.

   Warning 2: we do not provide all of the test cases you need to pass the autograder tests. If you do not write your own in addition to the ones we provide, you will lose a substantial fraction of your unit test points.

   Hint: to convert a character into its integer counterpart, use the Character.getNumericValue method.

   Files to Submit: Problem6.java, Problem6Test.java

7. (8 points) Wordle is a game created by Josh Wardle, where the objective is to guess a word with a given number of turns, inspired by Mastermind. In this exercise, you will implement a stage of the Wordle game.

   Design the String guessWord(String W, String G) method that, when given a string \(W\) and a "guess" string \(G\), returns a new string with the following properties:

   • If \( |W| \neq |G| \), return null.

   • For every index \( i \), if \( W_i = G_i \), append \( W_i \) to the output string. If \( W_i \neq G_i \) but \( G_i \in W \), append an asterisk to the output string. Otherwise, output a dash.

   Below are some example inputs and outputs.

   guessWord("PLANS", "TRAP")  => null
   guessWord("PLANS", "TRAIN") => "--A-*"
   guessWord("PLANS", "PLANE") => "PLAN-"
   guessWord("PLANS", "PLANS") => "PLANS"
   guessWord("PLANS", "SNLPA") => "*****"
     

   Files to Submit: Problem7.java, Problem7Test.java

8. (8 points) Design the String substring(String s, int a, int b) method, which receives a string \(s\) and two integers \(a\), \(b\), and returns the substring between these indices, inclusive on \(a\) and exclusive on \(b\). If \(a < 0\), \(b > s\texttt{.length()}\), or \(a > b\), return null.

   Warning: you cannot use the substring method(s) provided by the String class.

   Files to Submit: Problem8.java, Problem8Test.java

9. (8 points) File names are often compared lexicographically. For example, a file with name "File12.txt" is less than "File2.txt" because "1" is (lexicographically) less than "2".

   Design the int compareFiles(String f1, String f2) method that would fix this ordering to return the more sensible ordering. That is, if a file has a prefix and a suffix, where the only differing piece is the number, then make the file with the lower number return a negative number. You may assume that the file names are always of the form NameNum.Extension, where Name is some alphabetic string (i.e., where the string contains only letters), Num is some positive integer, and Extension is another alphabetic string. If the prefix or or suffix do not match, return the sign (i.e., -1, 0, 1) of calling compareTo on the entire strings. Take the following examples as motivation.

   compareFiles("File12.txt", "File1.txt")  => 1
   compareFiles("File10.txt", "File11.txt") => -1
   compareFiles("File1.txt", "File12.txt")  => -1
   compareFiles("File1.txt", "File1.txt")   => 0
   compareFiles("File1.txt", "File1.png")   => 1
   compareFiles("Docs.txt", "Files.png")    => -1
     

   Warning: if you try to Google this problem (or use AI for this problem), it will almost certainly tell you to use regular expressions or some other ridiculous approach. If you do, you will receive a 0 on the problem set. Again, both of these are violations of the academic integrity policy. Don't give in. Solve it yourself, like you should for all other problems.

   Files to Submit: Problem9.java, Problem9Test.java

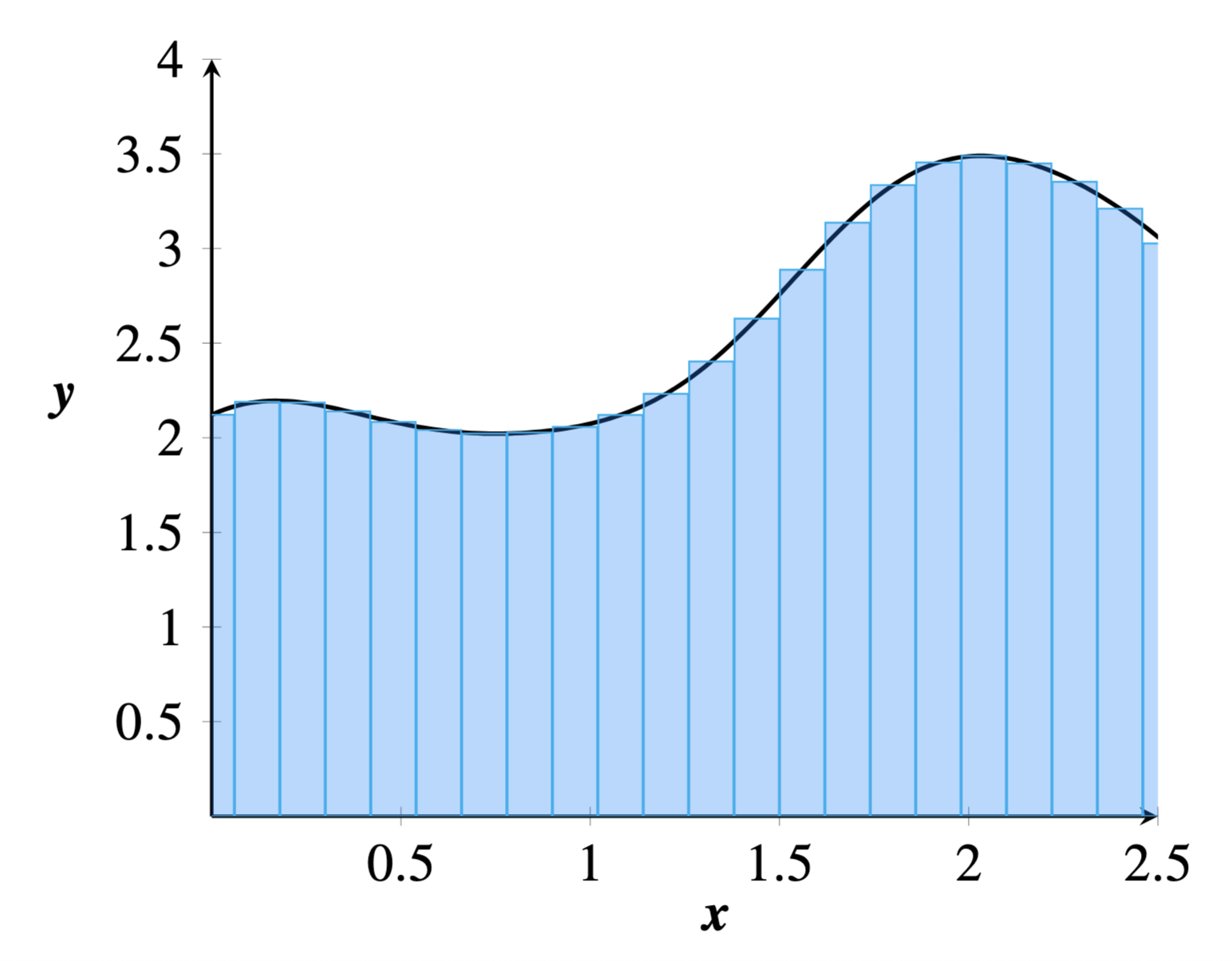
10. (16 points) The definite integral of a function \(f\), defined as \(\int_{a}^{b} f(x)\;\text{d}x\), produces the area under the curve of \(f\) on the interval \([a, b]\). The thing is, though, integrals are defined in terms of Riemann summations, which provide estimations on the area under a curve. Riemann sums approximate the area by creating rectangles of a fixed width \(\Delta\), as shown in Figure 1 for an arbitrary function \(f\). Left-Riemann, right-Riemann, and midpoint-Riemann approximations define the focal point, i.e., the height, of the rectangle. Notice that, in Figure 1, we use a midpoint-Riemann sum with \(\Delta = 0.2\), in which the collective sum of all the rectangle areas is the Riemann approximation. Your job is to use this idea to approximate the area of a circle.

    

    Figure 1: Midpoint-Riemann Approximation of a Function

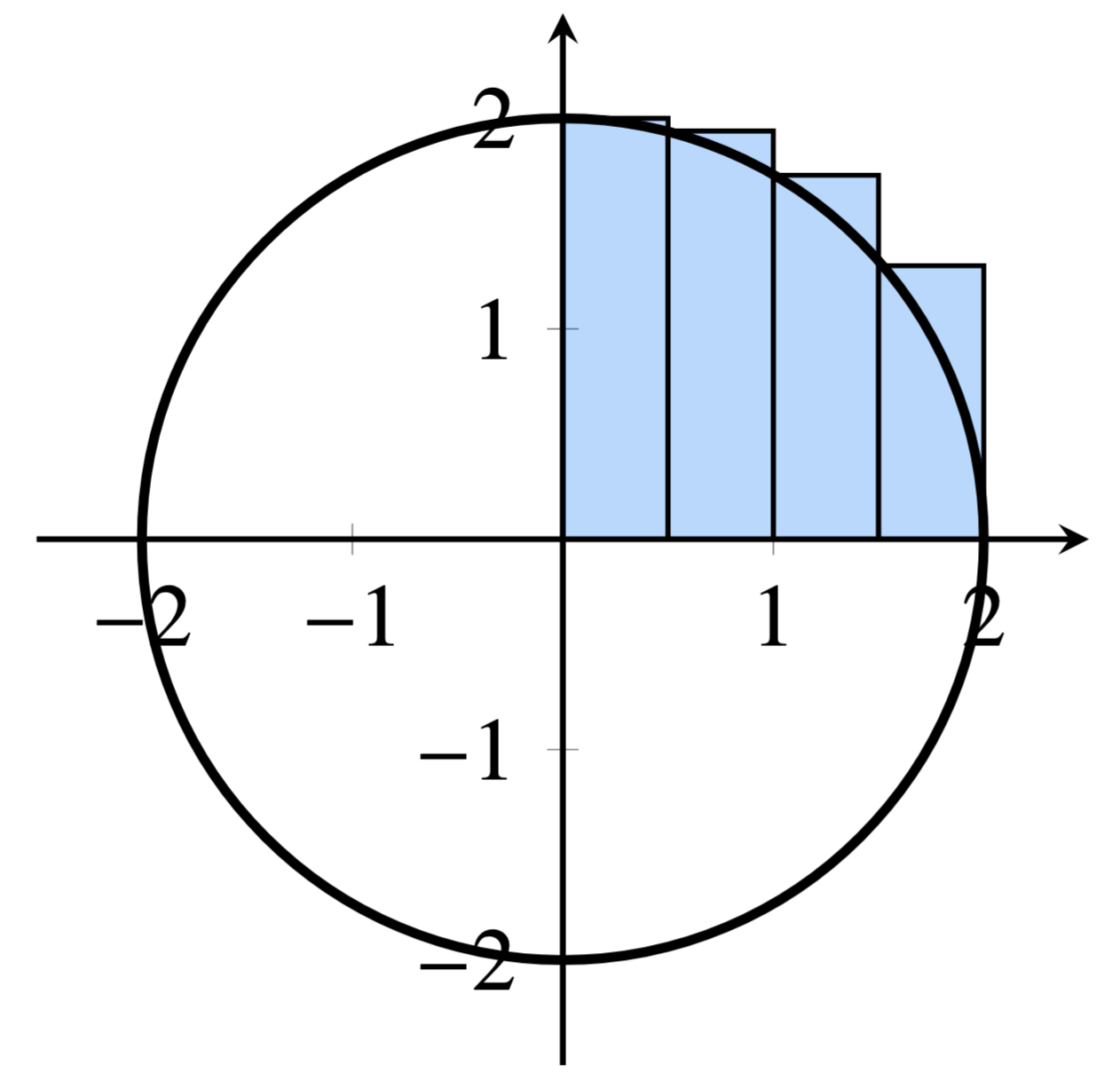
    Design the double circleArea(double r, double delta) method, which receives a radius \(r\) and a delta \(\Delta\). It computes (and returns) a left-Riemann approximation of the area of a circle. To solve this problem, compute the left-Riemann approximation of quadrant 1, and multiply the area by 4. We illustrate this in Figure 2 where \(\Delta=0.5\) and its radius \(r=2\). Further note that no calculus knowledge is necessary to solve this exercise.

    

    Figure 2: Left-Riemann Approximation of a Function

    Hint: remember the Pythagorean theorem?

    Files to Submit: Problem10.java, Problem10Test.java